Compositional Causal Reasoning Evaluation in Language Models

Causal reasoning and compositional reasoning are two core aspirations in AI. Measuring these behaviors requires principled evaluation methods. Maasch et al. 2025 consider both behaviors simultaneously, under the umbrella of compositional causal reasoning (CCR): the ability to infer how causal measures compose and, equivalently, how causal quantities propagate through graphs. CCR.GB applies the theoretical foundations provided by Maasch et al. 2025 to introduce new community datasets. CCR.GB provides a generative benchmark for measuring CCR at all three levels of Pearl's Causal Hierarchy: (1) associational, (2) interventional, and (3) counterfactual.

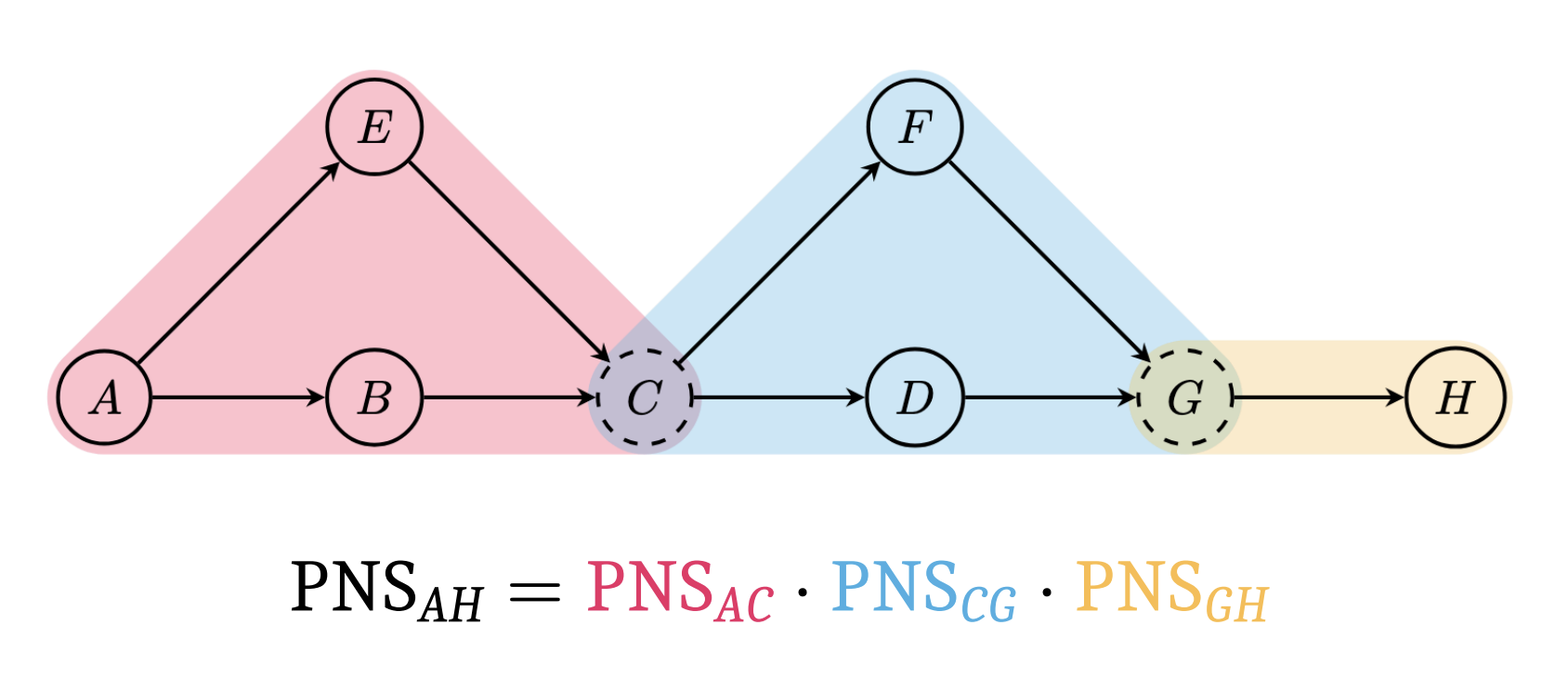
Pearl's Causal Hierarchy: observing factual realities, exerting actions to induce interventional realities, and imagining alternate counterfactual realities [Bareinboim et al. 2022]. Lower levels underdetermine higher levels. The counterfactual quantity $p(y'_{x'} \mid x,y)$ is known as the probability of necessity. CCR.GB uses a related counterfactual quantity, the probability of necessity and sufficiency, to evaluate AI reasoning [Pearl 1999].

CCR.GB provides two artifacts:

• Random CCR task generator. Open source code for on-demand task generation according to user specifications (graphical complexity, task theme, etc.). Find our task generators on GitHub. We currently offer four themes for random task generation: CandyParty, FluVaccine, FlowerGarden, and ClinicalNotes. The ClinicalNotes theme is currently our most complex prompt setup, and was designed in collaboration with a clinician to loosely resemble real-world history and physical (H&P) notes.
• Pre-sampled benchmark dataset. A static dataset sampled from the task generator, as a starting point for community benchmarking. Pre-sampled data can be found on Hugging Face. Currently, pre-sampled data are available for the ClinicalNotes and FluVaccine themes on simple causal graphs, but we encourage users to increase the graphical complexity of the tasks they randomly sample.

Quick start. See these Jupyter Notebook demos for a quick start on how to use our static dataset and task generators for evaluation, including recommended performance metrics. Additional helpful code can be found in our GitHub repository.

Future directions. CCR.GB is still under development. Future iterations will consider additional causal estimands and more complex task setups.

Key words. causal reasoning, compositional reasoning, graphical reasoning, clinical reasoning

• Compositionality + causality
• Disentangling signal from noise in causal reasoning evaluation
• CCR task generation
• LMs as counterfactual data simulators
• Performance metrics
• Taxonomy of reasoners
• How complex should the causal graph be?
• Preliminary results
• Paper slides
• How to cite this work (BibTeX)

We define CCR as the ability to correctly infer (1) how local causal measures compose into global causal measures and (2) how global causal measures decompose into local causal measures, in both factual and counterfactual worlds. By extension, this requires reasoning over the propagation of causal quantities through graphs. Thus, our framework also implicitly tests for graphical reasoning.

To facilitate CCR evaluation, we introduce a framework for the exhaustive assessment of compositional consistency: correct inference that equivalent compositions are indeed equal [Maasch et al. 2025]. We measure compositional consistency with respect to ground truth (external validity) and concordance among the LM's responses (internal consistency).

While explicitly combining compositional and causal reasoning evaluation in LMs is new, the intersection of compositionality and causality already enjoys a rich mathematical framework: the formalisms and methods of graphical modeling and causal inference. A classic example of compositionality in causal inference is the decomposition of the total effect in linear structural causal models (SCMs). When causal functions are linear, the total causal effect decomposes as a sum of the natural direct effect and natural indirect effect. A compositionally consistent causal reasoning agent should correctly infer that TE is equivalent to NDE + NIE:

Example 1: Decomposition of the total effect in linear SCMs.

In the current iteration of CCR.GB, we devise CCR tasks that leverage a particular compositional form of the probability of necessity and sufficiency (PNS; Pearl 1999).

As shown in Maasch et al. 2025, the PNS composes multiplicatively over the biconnected components of the causal DAG when each cause-effect pair of interest satisfies the monotonicity constraint noted above.

We exploit this property to construct reasoning tasks that require the LM to reason correctly over both local PNS values (e.g., $PNS_{AC}$) as well as their compositions. In the future, we aim to expand CCR.GB to incorporate additional compositional formulae for popular causal estimands.

Contemporary AI faces a persistent recall-reasoning gap. Closing this gap will require that genuine reasoning is rigorously differentiated from alternative phenomena, such as recall of previously seen information. CCR.GB is designed with this in mind.

• A generative approach. The automated task generator allows users to randomly sample new CCR tasks, mitigating risks that the model has seen a specific problem instance during training.
• Reasoning vs training data recall. Fictitious causal world models help prevent the conflation of recall and reasoning. Variables have no real-world counterparts, ensuring that newly-sampled causal relations were never seen by the model during training.
• Reasoning vs in-context recall. Compositional consistency evaluation helps disentangle in-context recall (e.g., extraction of relations directly from the causal context) from reasoning (e.g., inferring distal relationships that were never directly stated in the causal context).
• Causal reasoning vs numeracy. This benchmark contains both quantitative and qualitative CCR tasks (i.e., those requiring and not requiring numerical understanding, such as ordering numbers by magnitude). If an LM does significantly better on qualitative tasks, this might suggest that poor numeracy is one root of failure on quantitative CCR tasks. Currently, the ClinicalNotes and FlowerGarden themes offer qualitative prompts.

Lower error rate seen on factual questions (recall) than counterfactual questions (reasoning) [Hüyük et al. 2025].

When generating a custom CCR task, the user can specify the task theme, the graphical complexity of the causal DAG (total nodes, total biconnected components, connectivity), the desired causal functions (all logical or, all logical and, or randomly assigned), and the number of extraneous variables in the prompt (i.e., those not needed to solve the task). Each task is constructed as follows.

• Causal world model. First, we define a fictional world corresponding to a randomly generated causal graph. This will be the causal world model for the LM to reason over. The structural causal model defining our fictitious world is comprised of binary exogenous noise variables, binary endogenous variables, and nonlinear causal functions (monotonic logical operators and, or).
• Causal context prompt. Second, we construct a verbal description of the world model. This verbal description — our “causal context prompt” — contains all pertinent details needed for the LM to infer the world model, as well as extraneous details not needed to solve the CCR task. The causal context centers on a user defined theme (e.g., ClinicalNotes, CandyParty, FlowerGarden, FluVaccine, etc.).
• Sampling. Third, we randomly sample exogenous variables and extraneous variables and compute true endogenous variable values. Sampled values are then used to construct the "sample context" in natural language, which is concatenated to our causal context prompt. Each causal context will be copied many times, where each copy is paired with a new sample context.
• Factual query prompts. Next, we construct factual queries by treating the causal context + sample context as observational data. All queries are phrased as yes/no questions. The factual query is then concatenated to a copy of the causal context + sample context. Responses to factual prompts can be used to compute $p(y \mid x)$ for binary cause $x$ and binary effect $y$. Thus, evaluation on factual queries alone tests reasoning at the associational level of Pearl's Causal Hierarchy.
• Interventional query pairs. Finally, we construct paired interventional queries corresponding to interventions $do(X = True)$ and $do(X = False)$. Each interventional query is individually concatenated to a copy of the causal context + sample context. As with factual queries, all interventional queries are phrased as yes/no questions. Responses to interventional prompts are used to compute causal effects $p(y \mid do(X = True))$ and $p(y \mid do(X = False))$. As matched pairs over the exact same sample context (i.e., the same exogenous variable vector), these causal effects are also used to compute a counterfactual quantity: the PNS, $p(y_x,y'_{x'})$. In this setting, the PNS is equivalent to $p(y \mid do(X = True)) - p(y \mid do(X = False))$ (as $Y$ is monotonic in $X$). Thus, evaluation on interventional prompts tests for reasoning at both the interventional and counterfactual rungs of Pearl's Causal Hierarchy.

Instead of directly prompting the model to perform formal causal inference (as in Jin et al. 2023), CCR.GB treats LMs as counterfactual data simulators (as in Gonzalez and Nori 2024, Hüyük et al. 2025). Series of yes/no questions are submitted to the LM, and the natural language responses are converted to their corresponding boolean value (e.g., using another LM as an extracter; see Hüyük et al. 2025, Maasch et al. 2025). The resulting boolean vectors are treated as samples from observational and interventional distributions. These boolean vectors are then used to compute PNS estimates, or classic performance metrics such as F1 score, precision, and accuracy.

Responses generated using CCR.GB allow for reasoning evaluation at all three levels of Pearl's Causal Hierarchy.

• Associational.
• Metrics. Classic metrics can be used to compare factual query response vectors to ground truth (e.g., F1, accuracy, precision, etc.). This can also be considered a measure of logical reasoning, as causal functions are logical operators.
• Interventional.
• Metrics. Classic metrics like F1 score can also be used to compare interventional response vectors to ground truth.
• Counterfactual.
• Metrics. To assess counterfactual reasoning, we can estimate the PNS from the paired interventional response vectors and compare these estimates to the ground truth PNS for each quantity of interest in our causal world model. Approximation errors can be measured as the user desires, though we use the relative absolute error (RAE). We compute the RAE for the external validity of PNS estimates:
  
  

  

  
  and for the internal consistency of PNS compositions:
  
  

  

A note on sample size. If evaluating an LM at the associational or interventional levels using classic metrics like F1 score, the user can choose to evaluate on any number of queries that suits their needs. If evaluating at the counterfactual level to holistically assess the internal consistency and external validity of CCR over the full causal structure, a relatively large number of sample contexts must be represented. The appropriate sample size will vary by complexity of the causal structure. For example: for each causal quantity of interest, Maasch et al. (2025) sampled 1k sets of exogenous variables and replicated each five times. Such relatively large sample sizes are needed to preserve the compositional properties of the PNS in the finite sample setting. Thus, CCR evaluation at the counterfactual level is more expensive than (non-compositional) interventional and associational reasoning evaluation.

Through the lens of compositional consistency – the ability to reason that theoretically equivalent compositions are indeed equal – this evaluation framework is able to reveal a range of taxonomically distinct error patterns. Arising from the notions of external validity and internal consistency described above, Maasch et al. (2025) introduce a four-category taxonomy for compositional reasoning errors: valid-consistent, valid-inconsistent, invalid-consistent, and invalid-inconsistent. This taxonomy can be used to categorize model performance on CCR.GB tasks, providing insights for further error analysis. See Maasch et al. (2025) for elaboration.

As LMs become more capable, CCR.GB is more likely to be saturated. As shown in our preliminary results section and in Maasch et al. (2025), Llama models up to version 3.1 perform poorly even on very simple CCR tasks, GPT-4o does poorly without CoT plus demonstration, and o1 does well. For further context, we provide results from more recent reasoning models on a simple FluVaccine task. While DeepSeek R1 outperformed o4-mini and GPT-4o overall, no model showed perfect interventional reasoning even on this simple structure.

These results can be used as a baseline for deciding what level of graphical complexity might be appropriate for your models of interest. If testing on state-of-the-art reasoning models, we recommend that users opt for moderately-to-significantly more complex causal DAGs than this example.

As proof of concept, Maasch et al. (2025) demonstrate the design of CCR tasks for language models in the LLama, Phi, and GPT families. On a simple math word problem, this framework revealed a range of taxonomically distinct error patterns. Additionally, CCR errors increased with the complexity of causal paths for all models except o1.

Causal DAG of the simple CandyParty task used in Maasch et al. (2025).

Preliminary error analyses revealed several failure modes:

• Failure to correctly extract causal relations.
• Incorrect logic despite correct causal relation extraction.
• Truncated reasoning processes.
• Poor numeracy.

Results validate the utility and correct implementation of our framework, where success can be achieved by a sufficiently capable LM (e.g., o1 on the simple toy task). We recommend that users push the limits of the next wave of reasoning models by sampling increasingly complex causal DAGs from our task generator.

See Maasch et al. 2025 for further discussions of preliminary results.

The authors thank Dr Samuel M. Roh DMD, MD for insightful feedback on the structure of our ClinicalNotes task, which is loosely based on the format of real-world H&P notes.